Quick Sort
1. Quick Sort
퀵 정렬(quick sort)은 다음과 같은 특징을 가집니다.
- 불안정 정렬이며 분할 정복 알고리즘 중 하나로 평균적으로 매우 빠른 수행 속도를 가집니다.
- 불안정 정렬은 중복되는 원소가 기존 순서에 맞게 정렬되는 것을 보장하지 않는다는 의미입니다.
- 다른 원소와의 비교를 통해 정렬을 수행합니다.
- 추가적인 메모리 공간이 필요하지 않다.
- 이미 정렬된 리스트에 대해서는 불균형 분할이 수행되면서 수행 시간이 더 오래 걸립니다.
- 평균적으로 O(n log n), 최악의 경우 O(pow(n, 2)) 수행 시간이 걸립니다.
2. Process of Quick Sort
오름차순 기준 퀵 정렬은 다음과 같은 과정을 통해 수행됩니다.
- 리스트 가운데서 하나의 원소를 고릅니다.
- 고른 원소를 피벗(pivot)이라고 합니다.
- 피벗 앞에는 피벗보다 값이 작은 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 원소들이 오도록 정렬하면서 리스트를 둘로 나눕니다.
- 정렬을 마친 뒤에 피벗은 더 이상 움직이지 않습니다.
- 분할된 두 개의 작은 리스트에 대해 재귀(Recursion)적으로 이 과정을 반복합니다.
- 재귀는 리스트의 크기가 0이나 1이 될 때까지 반복됩니다.
퀵 정렬은 분할 정복(divide and conquer) 전략을 사용합니다. 분할 정복은 다음과 같은 과정을 통해 수행됩니다.
- 분할(Divide)
- 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분으로 나눕니다.
- 오름차순을 예로 들면 피벗을 기준으로 왼쪽엔 작은 값, 오른쪽엔 큰 값으로 나뉩니다.
- 정복(Conquer)
- 부분 배열을 정렬합니다.
- 부분 배열의 크기가 충분히 작지 않으면 재귀적으로 분할을 수행합니다.
- 결합(Combine)
- 정렬된 배열들을 하나의 배열로 합병합니다.
3. Practice
퀵 정렬을 통해 정수 배열을 오름차순으로 정리합니다.
3.1. sort method
- 왼쪽 인덱스가 오른쪽 인덱스보다 작은 경우에만 수행합니다.
- 왼쪽 인덱스와 오른쪽 인덱스를 기준으로 배열을 정렬합니다.
- 결과 값은 새로운 피벗 인덱스입니다.
- 왼쪽 인덱스와 피벗 인덱스를 기준으로 배열을 재귀적으로 정렬합니다.
- 피멋 인덱스와 오른쪽 인덱스를 기준으로 배열을 재귀적으로 정렬합니다.
void sort(int[] array, int left, int right) {
if (left < right) {
int pivotIndex = divideAndConquer(array, left, right);
sort(array, left, pivotIndex - 1);
sort(array, pivotIndex + 1, right);
}
}
3.2. divideAndConquer method
- 배열의 맨 왼쪽(left) 값을 피벗으로 지정합니다.
- 왼쪽 인덱스(left index)를 지정합니다.
- 오른쪽 인덱스(right index)를 지정합니다.
- 왼쪽 인덱스가 특정 조건을 만족하는 동안 증가합니다.
- 왼쪽 인덱스가 배열 맨 오른쪽(right) 위치를 넘지 않습니다.
- 왼쪽 인덱스에 위치한 값이 피벗 위치의 값보다 작습니다.
- 즉, 배열 맨 오른쪽 위치를 넘어가지 않는 선에서 피벗 위치 값보다 커지는 경우 반복문이 종료됩니다.
- 오른쪽 인덱스가 특정 조건을 만족하는 동안 감소합니다.
- 오른쪽 인덱스가 배열 맨 왼쪽 위치를 넘지 않습니다.
- 오른쪽 인덱스에 위치한 값이 피벗 위치의 값보다 큽니다.
- 즉, 배열 맨 왼쪽 위치를 넘어가지 않는 선에서 피벗 위치 값보다 작아지는 경우 반복문이 종료됩니다.
- 왼쪽 인덱스와 오른쪽 인덱스가 교차되지 않았다면 두 값을 교체합니다.
- 위 과정을 왼쪽 인덱스와 오른쪽 인덱스가 교차될 때까지 계속 반복합니다.
- 오른쪽 인덱스가 중앙 값의 위치를 가르키고 있으므로 피벗 위치의 값과 교체합니다.
- 정렬 위치의 새로운 기준이 되는 오른쪽 인덱스를 반환합니다.
void swap(int[] array, int from, int to) {
int temp = array[from];
array[from] = array[to];
array[to] = temp;
}
int divideAndConquer(int[] array, int left, int right) {
int pivot = left;
int leftIndex = left;
int rightIndex = right + 1;
do {
// pivot 위치의 값보다 작으면 skip
do {
leftIndex++;
} while (leftIndex <= right && array[leftIndex] < array[pivot]);
// pivot 위치의 값보다 크면 skip
do {
rightIndex--;
} while (left <= rightIndex && array[rightIndex] > array[pivot]);
// leftIndex, rightIndex 값이 교차되지 않았다면 값 변경
if (leftIndex < rightIndex) {
swap(array, leftIndex, rightIndex);
}
} while (leftIndex < rightIndex);
// pivot 위치의 값과 rightIndex 위치의 값을 변경
swap(array, pivot, rightIndex);
return rightIndex;
}
3.3. Test
- 정수 배열을 만들고 sort 메서드를 통해 정렬합니다.
- 배열의 값이 순서에 맞게 정렬되었는지 확인합니다.
@Test
void quick_sort_ascending_integer_array() {
int[] array = new int[]{6, 2, 5, 9, 1, 3, 10, 11, 4, 0, -1, 20, 7, 5, 1};
sort(array, 0, array.length - 1);
assertThat(array[0], equalTo(-1));
assertThat(array[1], equalTo(0));
assertThat(array[2], equalTo(1));
assertThat(array[3], equalTo(1));
assertThat(array[4], equalTo(2));
assertThat(array[5], equalTo(3));
assertThat(array[6], equalTo(4));
assertThat(array[7], equalTo(5));
assertThat(array[8], equalTo(5));
assertThat(array[9], equalTo(6));
assertThat(array[10], equalTo(7));
assertThat(array[11], equalTo(9));
assertThat(array[12], equalTo(10));
assertThat(array[13], equalTo(11));
assertThat(array[14], equalTo(20));
}
4. Difference between Merge Sort and Quick Sort
퀵 정렬과 합병 정렬의 차이점을 비교해보았습니다.
- 퀵 정렬은 균등 분할이 아닙니다.
- 추가적인 메모리가 필요하지 않습니다.
- 합병 정렬과 반대로 퀵 정렬은 먼저 정렬 후 분할을 수행합니다.
5. Time Complexitiy of Quick Sort
퀵 정렬 시간 복잡도 계산에 관련된 내용을 추가적으로 정리해보았습니다.
퀵 정렬은 최악과 최적의 경우에 따라 속도 차이가 많이 납니다.
좋은 피벗 결정이 정렬 속도를 좌지우지합니다.
설명을 위해 정렬할 아이템 개수가 n(=pow(2, k))개 있다고 가정하겠습니다.
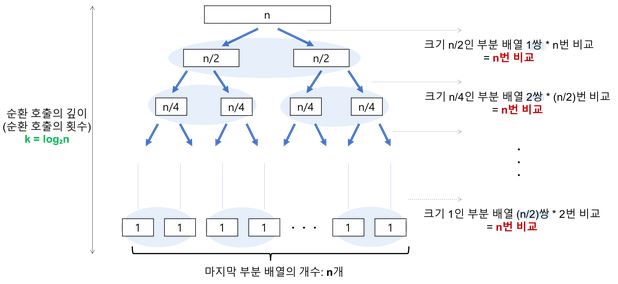
5.1. Using The Best Pivot
- 피벗에 의해 적절하게 배열이 이등분되는 경우입니다.
- 분할되는 재귀 함수의 깊이는
k(=log2(n))입니다. - 각 깊이 별로 값 비교를 n번 수행합니다.
- 계산되는 시간 복잡도는 다음과 같습니다.
- = 깊이 X 각 깊이별 비교 횟수
- = n X log2(n)
5.2. Using The Worst Pivot
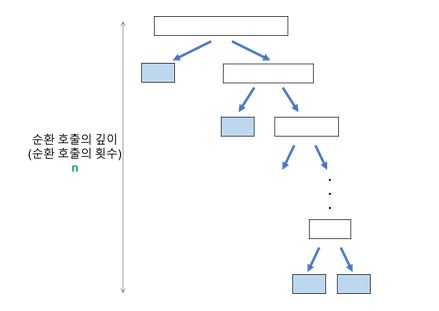
- 이미 정렬된 배열에서 피벗을 선택하는 경우 배열이 균일하지 않게 이등분되는 경우입니다.
- 피벗에 의해 길이가 1, n-1 인 배열 두 개로 나뉩니다.
- 분할되는 재귀 함수의 깊이는
k(=n)입니다. - 각 깊이 별로 값 비교를 n번 수행합니다.
- 계산되는 시간 복잡도는 다음과 같습니다.
- = 깊이 X 각 깊이별 비교 횟수
- = n X n

댓글남기기