Merge Sort
1. Merge Sort
합병 정렬(merge sort)은 다음과 같은 특징을 가집니다.
- 안정 정렬이며, 분할 정복 알고리즘 중 하나입니다.
- 안정 정렬은 중복되는 원소가 기존 순서에 맞게 정렬되는 것을 의미합니다.
- 시간 복잡도 O(n log n)를 가집니다.
- 병합하는 과정에서 정렬된 아이템들을 담을 공간이 필요하여 메모리가 많이 사용됩니다.
2. Process of Merge Sort
합병 정렬은 다음과 같은 과정을 통해 수행됩니다.
- 리스트의 길이가 0, 1 이면 정렬이 완료된 것으로 봅니다.
- 그렇지 않은 경우에는 절반으로 리스트를 분할합니다.
- 각 부분의 리스트를 재귀적인 방법으로 계속 잘라나갑니다.
- 두 부분의 리스트를 다시 하나의 정렬된 리스트로 합병합니다.
합병 정렬은 분할 정복(divide and conquer) 전략을 사용합니다. 분할 정복은 다음과 같은 과정을 통해 수행됩니다.
- 분할(Divide)
- 입력 배열을 같은 크기의 2개의 부분 배열로 분할합니다.
- 정복(Conquer)
- 부분 배열을 정렬합니다.
- 부분 배열의 크기가 충분히 작지 않으면 순환 호출을 통해 배열을 분할합니다.
- 결합(Combine)
- 정렬된 부분 배열들을 하나의 배열에 합병합니다.
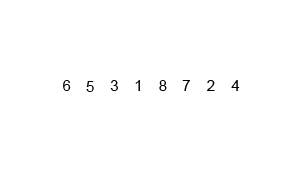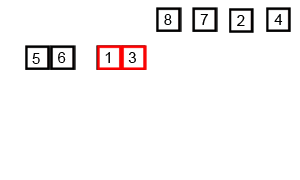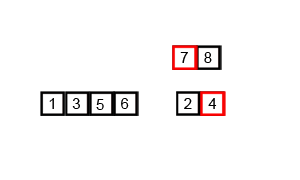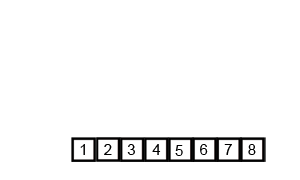
3. Practice
병합 정렬을 통해 정수 배열을 오름차순으로 정리합니다.
3.1. sort method
- 왼쪽 인덱스가 오른쪽 인덱스보다 작은 경우에만 수행합니다.
- 왼쪽, 오른쪽 인덱스 사이 중간 값을 기준으로 배열을 다시 나눠 정렬합니다.
sort메소드를 재귀적인 방법으로 호출합니다.
- 재귀적인
sort메소드 호출이 끝나면 배열이 정렬이 된 상태라고 판단합니다. - 중간 값을 기준으로 정렬된 배열을 왼쪽 인덱스에서 오른쪽 인덱스까지 함께 재정렬합니다.
public void sort(int[] array, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
sort(array, left, mid);
sort(array, mid + 1, right);
conquerAndCombine(array, left, right);
}
}
3.2. conquerAndCombine method
- 왼쪽, 오른쪽 인덱스 사이의 중간 값을 정합니다.
- 중간 값을 기준으로 왼쪽, 오른쪽 배열을 나눠 비교합니다.
- 크기가 작은 값을 임시 배열(temp array)에 저장합니다.
- 왼쪽, 오른쪽 배열 중 먼저 소비가 완료된 배열이 생기면 크기 비교 반복을 중단합니다.
- 왼쪽, 오른쪽 배열 중 소비가 완료되지 않은 배열이 있다면 이를 임시 배열에 마저 저장합니다.
- 모든 정렬이 완료되었으면 임시 배열의 값을 원래 배열에 복사합니다.
private void conquerAndCombine(int[] array, int left, int right) {
int mid = (left + right) / 2;
int[] tempArray = new int[right - left + 1];
int tempIndex = 0;
int leftIndex = left;
int rightIndex = mid + 1;
while (leftIndex <= mid && rightIndex <= right) {
if (array[leftIndex] < array[rightIndex]) {
tempArray[tempIndex++] = array[leftIndex++];
} else {
tempArray[tempIndex++] = array[rightIndex++];
}
}
while (leftIndex <= mid) {
tempArray[tempIndex++] = array[leftIndex++];
}
while (rightIndex <= right) {
tempArray[tempIndex++] = array[rightIndex++];
}
System.arraycopy(tempArray, 0, array, left, tempArray.length);
}
3.3. Test
- 정수 배열을 만들고
sort메소드를 통해 정렬합니다. - 배열의 값이 순서에 맞게 정렬되었는지 확인합니다.
package blog.in.action;
import blog.in.action.algoritm.MergeSort;
import org.junit.jupiter.api.Test;
import static org.hamcrest.MatcherAssert.assertThat;
import static org.hamcrest.Matchers.equalTo;
public class MergeSortTests {
@Test
void ascending_merge_sort() {
int[] array = new int[]{6, 2, 5, 7, 9, 1, 3, 4, 10, 11, 4};
MergeSort sut = new MergeSort();
sut.sort(array, 0, array.length - 1);
assertThat(array[0], equalTo(1));
assertThat(array[1], equalTo(2));
assertThat(array[2], equalTo(3));
assertThat(array[3], equalTo(4));
assertThat(array[4], equalTo(4));
assertThat(array[5], equalTo(5));
assertThat(array[6], equalTo(6));
assertThat(array[7], equalTo(7));
assertThat(array[8], equalTo(9));
assertThat(array[9], equalTo(10));
assertThat(array[10], equalTo(11));
}
}

댓글남기기