Calculate Number in Java

4 분 소요

0. 들어가면서

올 여름에 읽었던 이펙티브 자바 3/E에서 정확한 숫자 연산과 관련된 주의사항이 최근에 도움을 주었습니다. 금융 관련된 계산에 특히 주의하라는 조언이 있었는데, 마침 금융 프로젝트를 진행하게 되면서 잘못된 설계를 피해갈 수 있었습니다. 이번 포스트에선 Java에서 정확한 숫자 연산과 관련된 내용을 간략하게 정리해보려 합니다.

1. Binary Number

0과 1만으로 값을 표현하는 컴퓨터는 숫자를 이진법으로 표현합니다. 예를 들어 숫자 21을 이진수로 표현하면 10101가 됩니다.

10101 = (2^4 * 1) + (2^3 * 0) + (2^2 * 1) + (2^1 * 0) + (2^0 * 1)

이진법의 실수 표현

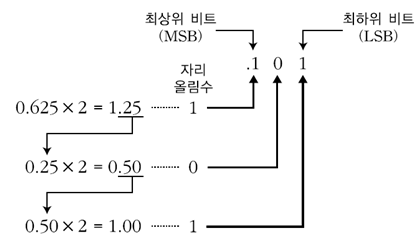
실수 표현은 헷갈릴 수 있는데, 원리는 동일합니다. 예를 들어 숫자 0.625를 이진수로 표현하는 방법은 다음과 같습니다.

0.625에 2를 곱하는 연산을 수행하여 1.25 값을 얻습니다.
이전 연산의 소수부인 0.25에 2를 곱하는 연산을 수행하여 0.5 값을 얻습니다.
이전 연산의 소수부인 0.5에 2를 곱하는 연산을 수행하여 1.0 값을 얻습니다.
이전 연산의 소수부는 0이므로 연산을 멈춥니다.
각 연산에서 얻어진 정수부(자리 올림수) 1, 0, 1를 순서대로 나열하면 소수부 이진수 표현이 됩니다.
숫자 0.625는 이진수로 표현하면 0.101이 됩니다.

0.101 = (2^-1 * 1) + (2^-2 * 0) + (2^-3 * 1)

https://suyeon96.tistory.com/9

2. Fixed Point and Floating Point

2.1. Fixed Point

컴퓨터는 자신의 연산 비트들을 갖고 최대한 다양한 값들을 표현하고자 다음과 같은 방법을 사용합니다. 컴퓨터가 실수를 표현하는 방법 중 고정 소수점(fixed point) 방식에 대해 먼저 알아보겠습니다. 32비트 기준으로 고정 소수점 방식에 대해 정리해보았습니다.

고정 소수점 표현

부호(1비트), 정수부(15비트)와 소수부(16비트)로 나눕니다.
정수부는 일반적인 이진수 표기법을 따릅니다.
소수부는 다음과 같은 규칙에 따라 표현됩니다.
숫자 7.625는 32비트 고정 소수점 표현으로 0 000000000000111 1010000000000000 입니다.
- 부호 0
- 정수부 111
- 실수부 101
- 나머지는 0으로 패딩(padding)

https://gguguk.github.io/posts/fixed_point_and_floating_point/

2.2. Floating Point

고정 소수점 방식은 표현할 수 있는 수의 범위가 좁기 때문에 컴퓨터는 실제로 부동 소수점(floating point) 방식을 사용합니다. 고정 소수점 방식과 다르게 소수점이 고정되어 있지 않습니다. 지수부(exponent)와 가수부(mantissa)를 만들고, 가수부의 소수점을 정규화를 통해 이동시킵니다. 예를 들어 7.625를 이진수로 표현한 111.101을 정규화하면 다음과 같습니다.

1.11101 * 2^2

밑수, 지수 그리고 가수 표현

부동 소수점 방식은 가수부와 지수부를 사용해 실수를 표현하는 방법입니다. 가수, 지수라는 용어가 익숙하지 않을 수 있으니 간단하게 정리해보겠습니다.

예를 들어 0.000012를 정규화하면 1.2 * 10^-5 값을 가집니다.
- 가수는 1.2 입니다.
- 밑수는 10 입니다.
- 지수는 -5 입니다.
위에서 구한 이진수 표현인 1.11101 * 2^2를 기준으로 설명하면 다음과 같습니다.
- 가수는 1.11101 입니다.
- 지수는 2 입니다.
- 밑수는 2 입니다.

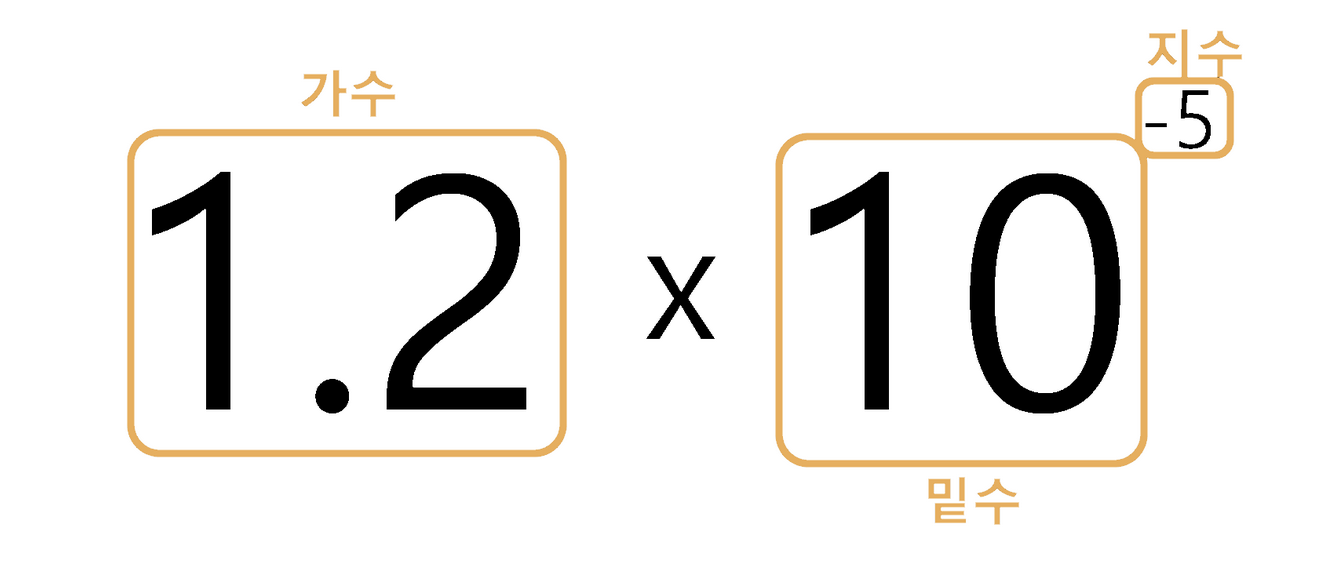
https:/taejunejoung.github.io/2019/12/24/java-primitive/

부동 소수점 표현

32비트 기준으로 부동 소수점 방식에 대해 알아보겠습니다.

부호(1비트), 지수부(8비트), 가수부(23비트)로 나눕니다.
지수부는 음의 지수를 처리하기 위해 편향(bias) 값을 127 더합니다.
- 지수부 0 ~ 127 구간은 음의 지수를 의미합니다. (-127 ~ 0)
- 지수부 128 ~ 255 구간은 양의 지수를 의미합니다. (1 ~ 128)
정규화 된 가수부를 표시합니다.
숫자 7.625는 32비트 부동 소수점 표현으로 0 10000001 11101000000000000000000 입니다.
- 부호 0
- 지수 (2 + 127) 값인 10000001
- 가수 1.11101 값에서 소수점 아래 11101

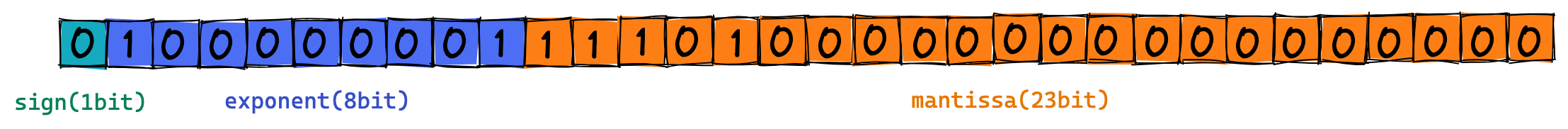
https://gguguk.github.io/posts/fixed_point_and_floating_point/

2.3. Expression Range

부동 소수점 방식은 고정 소수점 방식에 비해 표현할 수 있는 수의 범위가 굉장히 큽니다.

고정 소수점 방식
- 정수부가 15비트이므로 최대 65535 까지의 숫자만 표현 가능합니다.
- 실수부는 16비트이므로 131071개의 실수만 표현할 수 있습니다.
부동 소수점 방식
- 가장 작은 실수는 1.175494351E-38 까지 표현 가능합니다.
- 가장 큰 실수는 3.402823466E+38 까지 표현 가능합니다.

3. Floating Point Number in Java

컴퓨터는 실수를 정확하게 표현하지 못하는 한계를 가지고 있습니다.
비단 부동 소수점만의 문제는 아니지만, 어쨋든 부동 소수점 방식은 실수 연산이 부정확하다는 단점을 가지고 있습니다. (1/2)^n 의 합으로 정확하게 표현할 수 있는 실수는 많지 않습니다. Java에서 실수를 표현하는 float, double은 부동 소수점 방식을 사용하는데, 이를 사용한 연산은 부정확한 결과를 내놓습니다.

예를 들어 0.1을 이진수로 표현하면 0.0001100110011… 값을 가지는데, 소수점 아래 숫자가 정확하게 나눠 떨어지지 않고 순환됩니다. 컴퓨터는 숫자를 무한정으로 표현할 수 없기 때문에 가장 근사치 값이 사용됩니다.

부정확한 연산 처리

package app.number;

import org.junit.jupiter.api.Test;

import static org.hamcrest.MatcherAssert.assertThat;
import static org.hamcrest.Matchers.not;

public class NumberCalculateTests {

    @Test
    void wrong_number_calculate() {

        double number = 0;
        for (int i = 0; i < 1000; i++) {
            number += 0.1;
        }


        assertThat(number, not(100.0)); // 99.9999999999986
        assertThat(1.03 - 0.42, not(0.61)); // 0.6100000000000001
        assertThat(1.00 - 9 * 0.10, not(0.1)); // 0.09999999999999998
    }
}

4. BigDecimal 클래스

Java에서 정확한 계산 결과가 필요한 경우 BigDecimal, int, long 타입을 권장합니다. BigDecimal 클래스는 다음과 같은 상황에 사용할 수 있습니다.

소수점 연산이 필요한 경우
성능에 크게 문제가 없는 경우
19자리 이상 숫자를 다뤄야 하는 경우

int, long 타입은 다음과 같은 상황에 사용할 수 있습니다.

성능이 민간한 경우
소수점 계산을 직접 추적할 수 있고, 숫자가 크지 않는 경우
int 타입은 9자리, long 타입은 18자리 미만의 숫자를 다루는 경우

정확한 연산 처리

package app.number;

import org.junit.jupiter.api.Test;

import java.math.BigDecimal;

import static org.hamcrest.MatcherAssert.assertThat;
import static org.hamcrest.Matchers.equalTo;
import static org.hamcrest.Matchers.not;

public class NumberCalculateTests {

    @Test
    void correct_number_calculate() {

        BigDecimal number = BigDecimal.ZERO;
        for (int i = 0; i < 1000; i++) {
            number = number.add(BigDecimal.valueOf(0.1));
        }


        assertThat(number, equalTo(BigDecimal.valueOf(100.0)));
        assertThat(BigDecimal.valueOf(1.03).subtract(BigDecimal.valueOf(0.42)), equalTo(BigDecimal.valueOf(0.61)));
        assertThat(BigDecimal.valueOf(1.00).subtract(
                BigDecimal.valueOf(9).multiply(BigDecimal.valueOf(0.10))
        ), equalTo(BigDecimal.valueOf(0.1)));
    }
}

BigDecimal 클래스 주의사항

BigDecimal 생성자를 사용하는 방법은 값이 부정확할 수 있습니다. valueOf 메소드를 사용하는 것을 권장합니다.

package app.number;

import org.junit.jupiter.api.Test;

import java.math.BigDecimal;

import static org.hamcrest.MatcherAssert.assertThat;
import static org.hamcrest.Matchers.equalTo;
import static org.hamcrest.Matchers.not;

public class NumberCalculateTests {

    @Test
    void using_valueOf_method() {
        BigDecimal number1 = BigDecimal.valueOf(12.23);
        BigDecimal number2 = BigDecimal.valueOf(0.1);
        BigDecimal number3 = new BigDecimal("12.23");
        BigDecimal number4 = new BigDecimal("0.1");
        BigDecimal dontDoThis1 = new BigDecimal(12.23);
        BigDecimal dontDoThis2 = new BigDecimal(0.1);

        System.out.println(number1); // 12.23
        System.out.println(number2); // 0.1
        System.out.println(number3); // 12.23
        System.out.println(number4); // 0.1
        System.out.println(dontDoThis1); // 12.230000000000000426325641456060111522674560546875
        System.out.println(dontDoThis2); // 0.1000000000000000055511151231257827021181583404541015625
    }
}

TEST CODE REPOSITORY

https://github.com/Junhyunny/blog-in-action/tree/master/2022-11-23-calculate-number-in-java

REFERENCE

Twitter Facebook LinkedIn

강준현